使用O(1)时间复杂度计算比x大的最小的2的整数次幂

提到快速计算比给定整数 x 大（或相等）的最小的 2 ** n 的方法，一般来讲，我们都会这么算：

1
2
3

function minPowerOf2(x) {
    return Math.pow(2, Math.ceil(Math.log(x) / Math.log(2)));
}

或者有的数学功底不扎实的人可能就会这么写：

function minPowerOf2(x) {
    let power = 1;
    for(;;) {
        if(power >= x)
            return power;
        power *= 2;
    }
}

看看这个 for，看看这个倍增的变量，时间复杂度显然是 \(\Theta(\log n)\) 的。但是它实在是太慢了！有没有 \(\Theta(1)\) 的办法呢？

答案是：有。

const epsR = 2 ** 53;  // eps^-1
function minPowerOf2(x) {
    const base = epsR * x;
    const deviation = Math.abs(base + x - base);
    if(deviation === 0) return Math.abs(x);  // 也可以自己实现 abs() 函数
    return deviation;
}

跑跑看：

1 2	> minPowerOf2(1000) 1024

有点反直觉，但是确实工作了。这是什么原理呢？

背景知识介绍#

首先我们一眼可以看出 epsR 是 Number.MAX_SAFE_INTEGER + 1。这个数字是 IEEE 754 标准下双精度浮点数（64 bits）所能精确表示的最大整数：

[63]	[62:52]	[51:0]
S（符号位）	E（阶码位）	M（小数位）
0 表示正，1 表示负	1~2046	任意

其中，指数 \(E\) 的所有比特位为全 0 或全 1 时有特殊定义：

0b00000000000 = 0x000 用于表示 signed zero （当 \(F = 0\) 时）和 subnormals （当 \(F \ne 0\) 时）；
0b11111111111 = 0x7ff 用于表示 ∞ （当 \(F = 0\) 时）和 NaNs （当 \(F \ne 0\) 时）。

不过，以上两种情况都和本算法关系不是特别大，可以不用考虑。

二进制和十进制换算#

对于二进制小数数 \(\rm 101.01b\)，我们可以将其按照如下规则转换为十进制数 \(5.25\)： \[ \begin{aligned}5.25=1\times2^2+0\times2^1+1\times2^0+0\times2^{-1}+1\times2^{-2}\end{aligned} \] 所以我们可以将双精度浮点数的十进制形式表示为： \[ \begin{aligned}(-1)^S\times2^{E-1023}\times\left(1+\sum_{n=1}^{52}\left(M_n\times2^{-n}\right)\right)\end{aligned} \] 从双精度浮点数的二进制定义及十进制表示里，我们能发现当阶码位 \(E\) 越小时，所能精确表示的数字在数轴上就越密；随着 \(E\) 逐渐增大，能精确表示的数字在数轴上分布越来越稀疏。这是因为 \(\left(1+\sum_{n=1}^{52}\left(M_n\times2^{-n}\right)\right)\) 的取值范围恒为 \(\left[0, 2\right)\) 。事实上，在双精度浮点数所能表示的最小数字和最大数字之间，超过 \(99\%\) 的小数点后不超过 16 位的小数无法被双精度浮点数表出或精确表出。

举例，不能精确表出的：\(0.1_D=0.0\dot001\dot1_B\)，是一个二进制无限循环小数。
不能表出的：根据 信息论，\(N \,\rm bits\) 能表示的数字最多只有 \(2^N\) 个，无论是整数还是小数。

那么我们可以知道，52 个小数位最多能表示出 \(2^{52}\) 个数，而 \(2^{52}\) 到 \(2^{53}-1\) （包含首尾）总共就包括 \(2^{52}\) 个整数。这也是为什么常量 MAX_SAFE_INTEGER 的值是 2 ** 53 - 1：比 MAX_SAFE_INTEGER 小的正整数可以被表出，但是不能保证每一个比它大的正整数都能被表出。

这里有一个问题：为什么能表示出的 \(2^{52}\) 个数正好与 \(2^{52}\) 到 \(2^{53}-1\) 上的每一个整数一一对应呢？而不是对应 x.5 或是别的什么小数？其实是因为当双精度浮点数 \(P\) 落在 \(2^{52}\) 到 \(2^{53}-1\) 之间时，\(P\) 的阶码位 \(E\) 是固定的，为 \(52 + 1023 = 1076\)。而小数位 \(M\) 的精度（后文统称最小粒度）是 \(2^{-52}\)，所以 \(P\) 的最小粒度正好是 \(2^{E-1023}\times2^{-52}=1\)。因此在这个范围内每个能被 1 整除的数字都可以与某一个双精度浮点数 \(P\) 一一对应。同理，随着指数从 52 逐渐变小，\(P\) 的最小粒度也会逐渐变小为 \(\frac{1}{2}\)（对应指数为 51）、\(\frac{1}{4}\)（对应 50）…… 最终，在 0 和 \(2^0=1\) 之间达到 \(\frac 1 {2^{52}}\)，也即 JS 中的 Number.EPSILON。综上所述，比 MAX_SAFE_INTEGER 小的正整数是绝对可以被精确表出的。

原理分析#

TL;DR 其实就相当于找双精度浮点数的最高位

为了方便理解这些代码在干什么，我找到了 GitHub Gist 里的现成的可以显示双精度浮点数的二进制表示的轮子，并根据 gist 评论区指正内容稍作修改：11e971a7

来看一个例子：x = 3。

首先，使用上面提到的代码将有用的信息都显示在屏幕上：

Expression	Value	Binary (IEEE754 Double)
x	3	0 10000000000 100..(45x0)..0000
epsR	9007199254740992	0 10000110100 000..(45x0)..0000
epsR * x	27021597764222976	0 10000110101 100..(45x0)..0000
*epsR x + x**	27021597764222980	0 10000110101 100..(45x0)..0001
deviation	4	0 10000000001 000..(45x0)..0000

显然，相比于 epsR，epsR * x 在 \(E\)（阶码位）和 \(M\)（小数位）上都有变化： - \(E\) 增大了 Math.floor(Math.log2(x)) - \(M\) 处理了 \(E\) 增加完之后剩下的那部分（epsR * x - 2 ** Math.floor(Math.log2(x))）

这两步对于常规的双精度浮点数都是完全 OK 的。然而 epsR 实在是太大，导致在处理 epsR * x + x 时，到第二步出现了问题：

对于 \(x = 3\) 这种情况，到第四步之后，想要表示 27021597764222980， \(E\) 的全部和 \(M\) 的第一位已经表示了 epsR * x，所以 \(M\) 的剩下位应该表示 x。然而 \(M\) 的剩下位不可能精确表示出 x 了：此时，阶码位 \(E\) 已经全部确定，使得十进制表达式中第二项固定为 \(2^{1077-1023}=2^{54}\)，要想表示出 3 则需要 \(M\) 的最小粒度变成 \(2^{-54}\)。然而因为 \(M\) 总共只有 52 位，所以只能苦哈哈地舍弃一部分精度，转换成比 epsR * x + x 大的、能精确表示的最接近 epsR * x + x 的数字。

—— 停一下！为什么到 epsR * x + x 时才出现误差？epsR * x 也超过 Number.MAX_SAFE_INTEGER 了啊？

—— 这是因为当 x 在 \([0, \texttt{epsR}-1]\) 也即 \([0, 2^{53}-1]\) 范围内时，Math.floor(Math.log2(x)) 的取值范围为 \([0, 52]\)，所以 epsR * x - 2 ** Math.floor(Math.log2(x)) 都可以被小数位 \(M\) 正确处理。

具体来讲，前文提到了 \(M \in [0, 2)\) 且根据十进制表示可知 \(M\equiv0\mod{2^{-52}}\)，所以对于任何比 \(\tt epsR\) 大的 \(\tt epsR\) 的正整数倍数 \(P\)，必然可以构造 \(P = (-1)^0\times2^{53\times A}\times M'\)，其中 \(A=\tt Math.floor(Math.log2(x))\) —— 这样，\(M'\) 的最小粒度 \(2^{-52}\) 乘以新增加的 \(2^A\,\,(A\in[0, 52])\)，可以得出 \(P\) 的最小粒度必然小于等于 1（且是 2 的整数次幂），所以对于每一个这样的 \(P\) 都存在一个双精度浮点数与之一一对应。

但是到了 epsR * x + x 时，这个性质不再被满足，就有可能出现误差。为了更好地展示这一点，我们可以观察一下 epsR * x + x 的 \(M\)（小数位）的最后几位是在何时被抛弃的。

理想情况下，不丢失精度的表示方式：

1
2
3

...00      1
//  ↑      ↑
//  最末位  虚构的比最末位还要末的位

实际的表达方式：

1
2
3

...01
//  ↑
//  最末位，四舍五入后发生进位

那么，只剩下最后一块拼图，就是为什么舍弃精度后 epsR * x + x 会转换成比 epsR * x + x 大的最小的双精度浮点数，而不是比 epsR * x + x 小的最大的双精度浮点数？（注：这里讨论的都是 x 不是 2 的正整数次幂的情况）

其实答案非常简单。不难看出此时阶码位 \(E\) 是由 epsR * x 确定的，因为 + x 部分太小了（\(\texttt{x} \in [0, 2^{53}-1]\)），不足以影响到 \(E\)。此时，存在 \(E-1023=53+\lfloor\log_{2}x\rfloor\)，故此时该双精度浮点数的最小粒度是 \(2^{1+\lfloor\log_{2}\texttt{x}\rfloor}=2\times2^{\lfloor\log_2\texttt{x}\rfloor}\) 也即「比 x 大的最小的 2 的正整数次幂」。所以 x 必然大于最小粒度的一半。

上述文字论述，可以转化为更直观的图表。在数轴上，存在如下几个数：

epsR乘以x附近的双精度浮点数.jpg

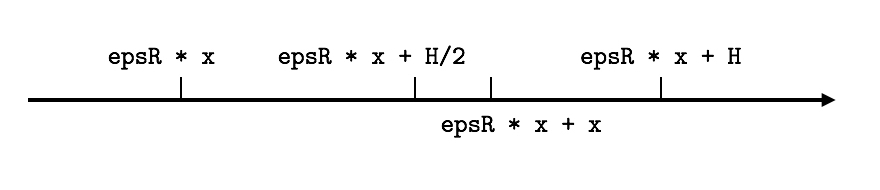
注意，epsR * x + H/2 不是双精度浮点数，图示仅仅是为了方便参考大小关系。

那么自然而然，舍入时就会舍入到「比 epsR * x + x 大的最小的双精度浮点数」上了，而不会舍入到更远的「比 epsR * x + x 小的最大的双精度浮点数」。

所以我们可以从这个例子出发，进行一些普适的论证：刚刚说到的这个新的数字就会等于 epsR * x 加上一个比 x 大的最小的能够满足 \(M\) 的最小粒度的数字了（我们就叫它数字 \(B\) 吧）；随着 \(2^{53\times A}\) 中的 \(A\) 不断变大，能满足 \(M\) 的最小粒度的 \(B\) 也会不断变大。又因为最终目标是 \(\min B=2^{53\times A}\times M\)，自然要想取到 \(B\) 的最小值，等价于取到 \(M\) 的最小值，也就是 \(2^{-52}\)。

所以，得到结论： \[ B=2^{53\times A\times-52}=2^{A+1}=2^{\tt Math.ceil(Math.log2(x))} \] 那么我们要想把 \(B\) 从「比 epsR * x + x 大的最接近它的双精度浮点数」里分离出来，自然就再减去一个 epsR * x 就可以了。因为「比 epsR * x + x 大的最接近它的双精度浮点数」和 epsR * x 都可以被双精度浮点数精确表出，所以这一步不会损失精度。

最后就得到了 \(B\)，也就是比 x 大的最小的 2 的正整数次幂。

补充说明：当 x 本身就是 2 的正整数次幂时，上述所有计算都不会有精度损失，所以最后返回的还是 x。因此本文标题为了严谨，给出的说法是「比给定整数 x 大（或相等）的最小的 2 的正整数次幂」。

来源：https://blog.jiejiss.com/

使用 O (1) 时间复杂度计算比 x 大的最小的 2 的整数次幂

文章目录

背景知识介绍#

二进制和十进制换算#

原理分析#