简述Bi-LSTM+CRF
主要也是最近刚在学校的某“人工智能研讨会”上展示了一个基于这玩意的项目,趁着还记得原理赶紧写下来。
Bi-LSTM
这玩意全称是双向长短时记忆网络(Bi-directional Long-Short Term Memory)。其架构为一个双向 RNN,其每一个 Cell 的激活函数都被置换为一个 LSTM Cell。
RNN
全称为 Recurrent Neural Network ,与传统神经网络的不同之处是自己可以传递权重给自己。大概像是这样:
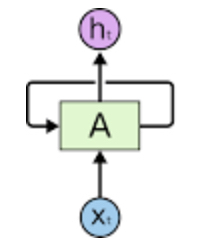
我们把它在时间上展开(横轴为时间),可以得到:
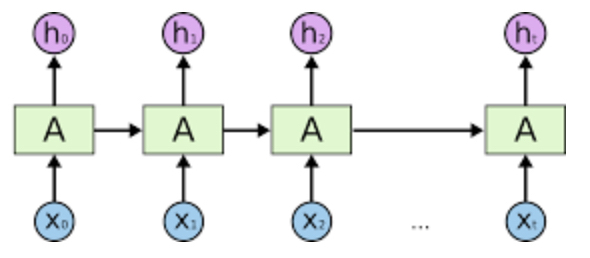
上图就是所谓的“上一秒的信息传递给下一秒的自己”。
在传统 RNN 里,每个 A 都是个激活函数,组网之后用 BPTT 算法暴力训练。
BPTT 算法使得梯度可以在时间通道上传递,但是由于局部梯度受过往梯度的累计影响是指数级的(设此时刻到下一时刻的权重为 \(s_t\),则 Sigmoid 对应的梯度递推公式为 \(\frac{\partial\,{\rm Loss}_t}{\partial\,s_{t-1}^*}=(s_{k-1}*(1-s_{k-1}))*(W^T\times \frac{\partial\,{\rm Loss}_t}{\partial\,s_t^*})\),显然 Sigmoid 的梯度 \(s_{k-1}*(1-s_{k-1})\) 会累乘起来,以指数的方式影响结果),所以容易引发梯度爆炸或者梯度消失的问题。解决梯度消失可以换用 ReLU,只不过更容易发生梯度爆炸。梯度爆炸则可以通过设置阈值来避免。另外一种解决的思路就是更改 Cell 的结构,如 LSTM 网络和 GRU 网络。补充知识:LSTM 训练比 GRU 慢,模型更大,但结果更好。GRU 是在对 LSTM 进行简化的基础上产生的,所以一般大家如果要用到 RNN,都会选择直接上 LSTM。
双向RNN
双向RNN其实就是两个反向的RNN共用一个输入层和输出层,像这样:
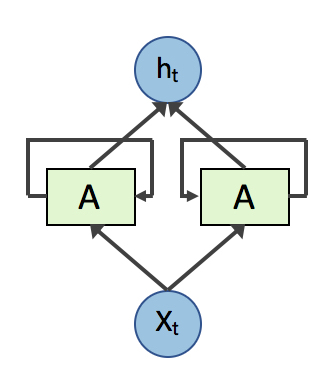
其在 RNN 基础上增加的优点仅仅是可以同时考虑上下文。(RNN 只能考虑之前的状态,BRNN 之前和之后的都能考虑)
LSTM
全称为 Long-Short Term Memory,是 RNN 的变种。在 LSTM 中,每一个 Cell A 都是这个样子的:
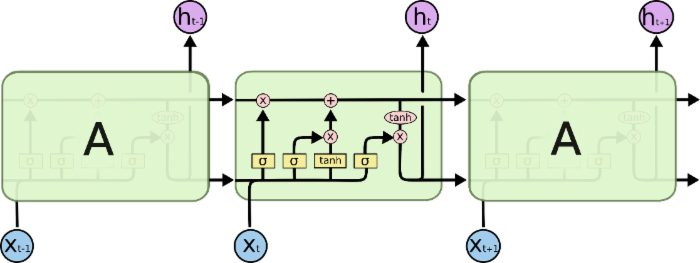
一个 LSTM Cell 内部有三个门(Gate),分别是遗忘门、输入门和输出门。LSTM 中信息的传递则是有设计专门的通道:
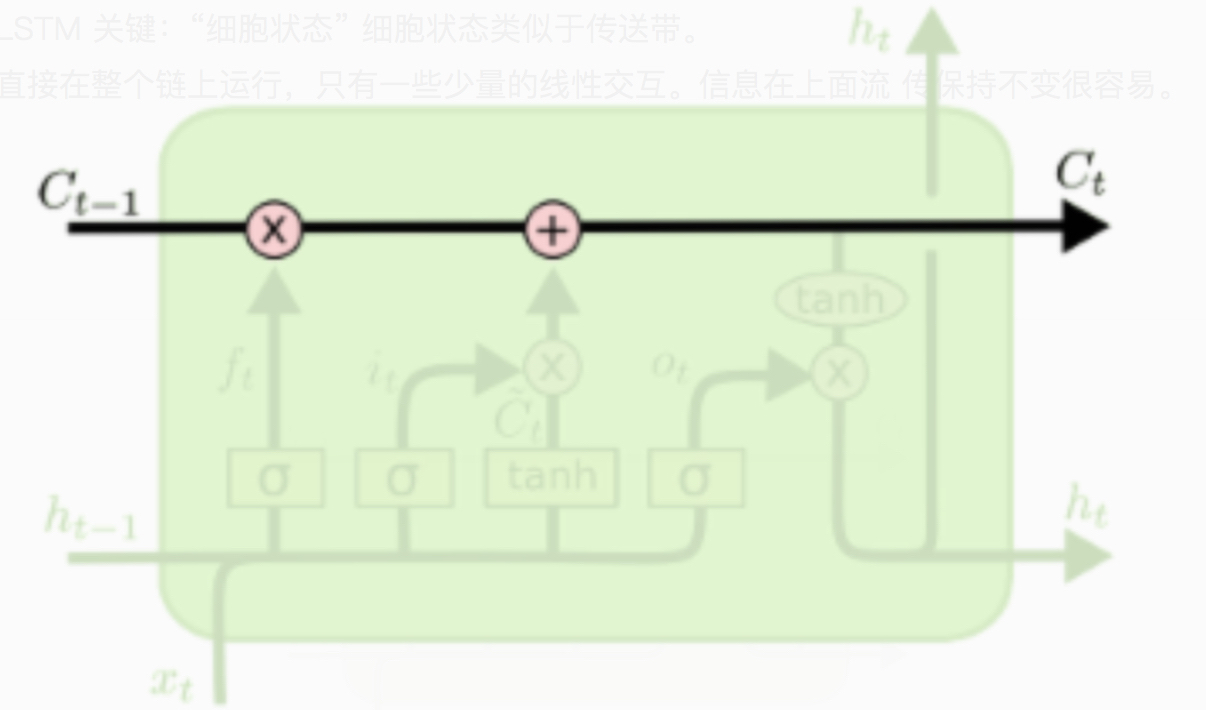
在这条通道上全部是线性运算,信息可以持续的传递下去,不会轻易改变或丢失。
遗忘门
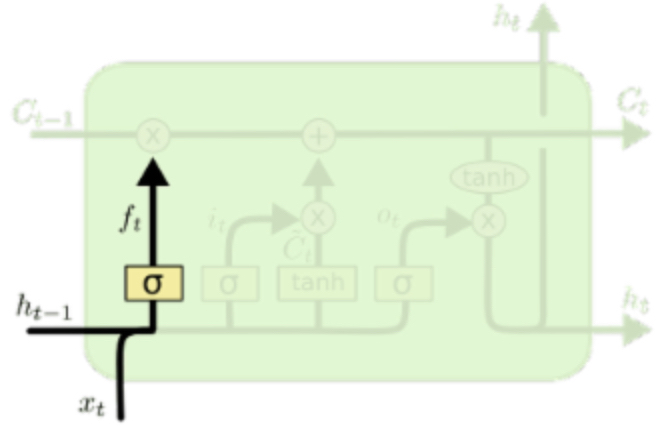
\(\sigma\) 是 Sigmoid 函数。于是很容易发现,上一时刻的 hidden state \(h_{t-1}\) 与此时刻的输入 \(x_t\) 级联之后,经过 Sigmoid 函数变换为一个 \((0, 1)\) 之间的值并与 \(C_{t-1}\) 相乘(element wise)。如果 \(\sigma\) 函数的输出 \(f_t\) 接近 0,相当于 \(C_{t-1}\) 这个信息被忘掉了。
选择 Sigmoid 函数是因为其在定义域上大部分取值接近 0 或 1,可以近似对应上遗忘/不遗忘。然而这里不能采用阶跃函数,因为阶跃函数的梯度为 0,无法梯度下降,对其求导也会导致梯度消失。在后面的门中选择 Sigmoid 的理由类似。
其中,\(f_t=\sigma(W_{f} \cdot [h_{t-1}, x_t]+b_f)\)。
输入门
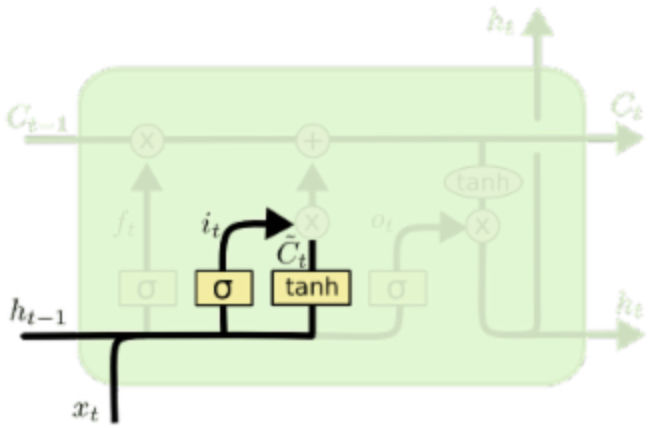
同样,\(h_{t-1}\) 与 \(x_t\) 级联之后经过 \(\sigma\) 的变换,与 \(\tanh\) 的输出相乘,并与之前的细胞状态 \(C_{t-1}* f_t\) 相加,得到最终的细胞状态 \(C_t\)。\(\tanh\) 存在的意义主要是为了将输入变换到 \((-1, 1)\) 之间,这样 \(\tilde C_t * i_t\) 各个元素仍然位于 \((-1, 1)\) 中,方能作为合法的细胞状态继续参与运算。如果 \(i_t\) 接近 0,那么意味着此输入没有加入到细胞信息中的必要,由于乘法的性质这个输入会被丢弃掉。
其中,\(i_t=\sigma(W_i\cdot [h_{t-1}, x_t]+b_i)\),\(\tilde C_t=\sigma(W_C\cdot [h_{t-1}, x_t]+b_C)\)。
输出门
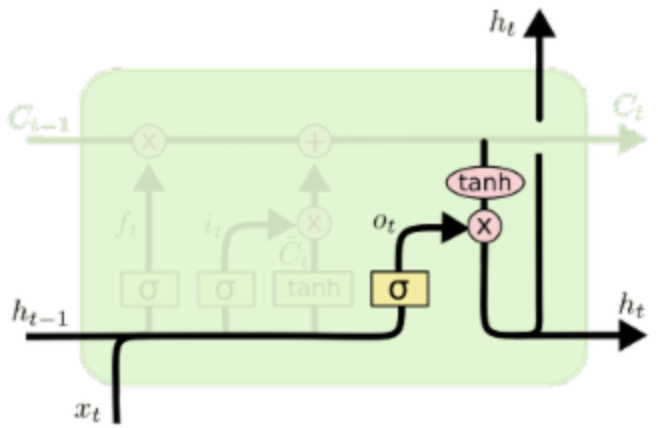
仍然是 \(h_{t-1}\) 与 \(x_t\) 级联之后经过 \(\sigma\) 的变换,与 \(\tanh(C_t)\) 相乘(仍然是 element wise),得到新的 hidden state \(h_t\)。这个门控制是否要输出细胞信息到 hidden state 中,如果 \(o_t\) 接近 0,则相乘完了仍然接近 0,相当于不会输出到 hidden state 里。\(\tanh\) 的作用依旧是为了将 \(C_t\) 中的元素映射到 \((-1,1)\) 内。
其中,\(o_t=\sigma(W_o \cdot [h_{t-1}, x_t]+b_o)\),\(h_t=o_t * \tanh(C_t)\)
总结
所以,Bi-LSTM 就是每个 Cell 都是 LSTM Cell 的双向 RNN。其拥有同时从上文和下文中提取信息的能力,并且相较于双向 RNN 正确率更高。
CRF
全称为 Conditional Random Field,条件随机场。本文中主要说的是线性链条件随机场(Linear Chain CRF)。
随机场(RF)的定义:随机场是由若干个位置组成的整体,当给每一个位置中按照某种分布随机赋予一个值之后,其全体就叫做随机场。
马尔科夫随机场(MRF)的定义:某个随机场,其中某一个位置的赋值仅仅与和它相邻的位置的赋值有关,和与其不相邻的位置的赋值无关,则该随机场是马尔科夫随机场(具有马尔科夫性)。
条件随机场(CRF)的定义:某个马尔科夫随机场,其中只存在两个变量 \(X\) 和 \(Y\),且 \(X\) 为自变量,\(Y\) 为因变量。则该马尔科夫随机场为条件随机场。
线性链条件随机场(Linear-CRF)的定义:某个条件随机场,其中的 \(X\) 和 \(Y\) 具有相同的维度,则该条件随机场为线性链条件随机场。
补充内容
Linear-CRF 的数学定义:
设 \(X=(X_1,X_2, \cdots,X_n)\),\(Y=(Y_1,Y_2,\cdots,Y_n)\) 均为线性链表示的随机变量序列,在给定随机变量序列 \(X\) 的情况下,随机变量 \(Y\) 的条件概率分布 \(P(Y|X)\) 构成条件随机场,也即满足马尔科夫性:
\[P(Y_i | X,Y_1,Y_2,\cdots,Y_n)=P(Y_i|X,Y_{i−1},Y_{i+1})\]
则称 \(P(Y|X)\) 为线性链条件随机场。
CRF 层以 Bi-LSTM 层的输出为输入,其可以通过学习数据集中不同 label 间的转移概率从而修正 Bi-LSTM 层的输出。例如,对于 BIO 模型,不存在 I 开头的词,也不存在连续两个 B。如果 Bi-LSTM 给出了上述输出,则 CRF 层可以基于转移概率矩阵对其进行修改。
当然,CRF 除了验证以外,还可用于预测和判断。不过这两个功能我的项目中没有涉及,所以本文中无法给出详细的解释,免得说错了贻笑大方。